2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test
-
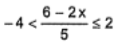
eşitsizliğinin çözüm kümesi nedir?A) [-13,2) B) (-13,2] C) [-2,13)
D) [2,9) E) (2,9]
-
a3b üç basamaklı sayısı 3ab üç basamaklı sayısından 90 fazla ise a kaçtır?
A) 2 B) 3 C) 4 D) 5 E) 6
-
a ve b pozitif tam sayılar olmak üzere,
2a + 3b = 27
eşitliğini sağlayan kaç farklı (a,b) ikilisi vardır?A) 3 B) 4 C) 5 D) 6 E) 7
-
a2 . b3 > 0
b5 . c3 < 0
a - c < 0
olduğuna göre a, b ve c reel sayılarıanın işaretleri sırası ile aşağıdakilerden hangisidir?A) -,+,- B) -,-,+ C) +,+,- D) +,-,- E) -,-,-
-
a,b,c birere tam sayı ve
a.b = 2c - 1
olduğuna göre, aşağıdakilerden hangisi doğrudur?A) a ve tek sayılardır
B) a ve b çift sayılardır
C) a çift, b tek sayıdır.
D) a - b tek sayıdır.
E) a + b tek sayıdır.
-
|x+2y-5| + (2x + y - 4)2=0
olduğuna göre, x.y kaçtır?A) 1/2 B) 1 C) 3/2 D) 2 E) 5/2
-
|x+2y-5| + (2x + y - 4)2=0
olduğuna göre, x.y kaçtır?A) 1/2 B) 1 C) 3/2 D) 2 E) 5/2
-
a.x - 3(x - 2) = 2(x + 1) + b
denkleminin çözüm kümesi tüm gerçek sayılar olduğuna göre a + b kaçtır?A) 0 B) 1 C) 5 D) 6 E) 9
-
p ' ∧ (p' v q)' önermesinin en sade hali aşağıdakilerden hangisidir?
A) 0 B) q C) q' D) 1 E) p
-
A = {1,2{1,2},3,{2,3}} kümesi veriliyor.
Buna göre aşağıdakilerden hangisi A kümesinin 3 elemanlı alt kümelerindne biri değildir?A) {2,{1,3},{2,3}} B) {1,2,{1,2}}
C) {2,3,{2,3}} D) {1,{1,2},{2,3}}
E) {1,{1},{1,3}}
-
Bir öğretmen, 30 öğrencisinin her birine bir Türkçe ve bir matematik ödevi vermiştir. Daha sonra öğretmen, ödevleri kontrol ettiğinde 12 öğrencisinin Türkçe ödevini 13 öğrencisinin matematik ödevini yapmadığını görmüştür.
Bu durumda yalnızca matematik ödevini yapan öğrenci sayısı 5 olduğuna göre her iki ödevini yapan öğrenci sayısı kaçtır?A) 11 B) 12 C) 13 D) 14 E) 15
-
A3B5 dör basamaklı sayısı 9 ile, A1B üç basamaklı sayısı 5 ile kalansız bölünebilmektedir.
Bu göre A'nın alabileceği değerler toplamı kaçtır?A) 3 B) 5 C) 8 D) 11 E) 13
-
Mehmet Bey, fiyatları eşit ve lira cinsinden tam sayı olan gömleklerin 9 tanesini 4A1 lira ödemiştir.
4A1 üç basamaklı bir doğal sayı olduğuna göre bir gömleğin fiyatı kaç liradır?A) 49 B) 48 C) 47 D) 46 E) 45
-
Doktor Mustafa 6 günde bir, hemşire Aslı 8 günde bir nöbet tutmaktadır.
İkisi birlikte Cuma günü nöbet tuttuktan sonraki 2.birlikte nöbetleri hangi gün olur?A) Salı B) Çarşamba C) Perşembe
D) Cuma E) Cumartesi
-
Bilinmeyeni x olan 2x + 3(x-a) - 1 = bx + 8 denkleminin çözüm kümesi sonsuz elemanlı olduğuna göre a + b kaçtır?
A) 2 B) 3 C) 8 D) 9 E) 11
-
4(x-5) + 2(x-12) - 3(-x +3) = 1 denkleminin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir?
A) {-18} B) {-6} C) {6} D) {18} E) {-24}
-
-5x + 7 ≤ -2x -14 eşitsizliğini sağlayan x'in en küçük tam sayı değeri kaçtır?
A) 8 B) 7 C) 4 D) 3 E) 0
-
|2x - 5| - 3 < 6 eşitsizliğini sağlayan kaç tane x tam sayısı vardır?
A) 7 B) 8 C) 9 D) 10 E) 11
-
3(x-2) + x -10 = -2x - 4 denkleminin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir?
A) {2} B) {-4} C) {-6} D) R E) ∅
-
Aşağıdakileden hangisi bir irrasyonel sayıdır?
A) 0,3- B) 1,75 C) √12 D) √16 E) √25
-
olduğuna göre a + b kaçtır? A) 10 B) 11 C) 12 D) 13 E) 14
-
||x - 4| + 2 | = 5 denkleminin çözüm kümesi aşağıdakilerden hangisisidir?
A) {-7, -1} B) {-7, 1} C) {-1, 7}
D) {1,7} E) {-1, -7}
-
denklem sistemini sağlayan x değeri kaçtır?A) 16 B) 12 C) 9 D) 6 E) 4
-
işleminin sonucu kaçtır? A) 2 B) √5 C) 3 D) 7 E) √8
2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test CEVAPLARI
-
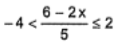
eşitsizliğinin çözüm kümesi nedir?A) [-13,2) B) (-13,2] C) [-2,13)
D) [2,9) E) (2,9] -
a3b üç basamaklı sayısı 3ab üç basamaklı sayısından 90 fazla ise a kaçtır?
A) 2 B) 3 C) 4 D) 5 E) 6
-
a ve b pozitif tam sayılar olmak üzere,
2a + 3b = 27
eşitliğini sağlayan kaç farklı (a,b) ikilisi vardır?A) 3 B) 4 C) 5 D) 6 E) 7
-
a2 . b3 > 0
b5 . c3 < 0
a - c < 0
olduğuna göre a, b ve c reel sayılarıanın işaretleri sırası ile aşağıdakilerden hangisidir?A) -,+,- B) -,-,+ C) +,+,- D) +,-,- E) -,-,-
-
a,b,c birere tam sayı ve
a.b = 2c - 1
olduğuna göre, aşağıdakilerden hangisi doğrudur?A) a ve tek sayılardır
B) a ve b çift sayılardır
C) a çift, b tek sayıdır.
D) a - b tek sayıdır.
E) a + b tek sayıdır. -
|x+2y-5| + (2x + y - 4)2=0
olduğuna göre, x.y kaçtır?A) 1/2 B) 1 C) 3/2 D) 2 E) 5/2
-
|x+2y-5| + (2x + y - 4)2=0
olduğuna göre, x.y kaçtır?A) 1/2 B) 1 C) 3/2 D) 2 E) 5/2
-
a.x - 3(x - 2) = 2(x + 1) + b
denkleminin çözüm kümesi tüm gerçek sayılar olduğuna göre a + b kaçtır?A) 0 B) 1 C) 5 D) 6 E) 9
-
p ' ∧ (p' v q)' önermesinin en sade hali aşağıdakilerden hangisidir?
A) 0 B) q C) q' D) 1 E) p
-
A = {1,2{1,2},3,{2,3}} kümesi veriliyor.
Buna göre aşağıdakilerden hangisi A kümesinin 3 elemanlı alt kümelerindne biri değildir?A) {2,{1,3},{2,3}} B) {1,2,{1,2}}
C) {2,3,{2,3}} D) {1,{1,2},{2,3}}
E) {1,{1},{1,3}} -
Bir öğretmen, 30 öğrencisinin her birine bir Türkçe ve bir matematik ödevi vermiştir. Daha sonra öğretmen, ödevleri kontrol ettiğinde 12 öğrencisinin Türkçe ödevini 13 öğrencisinin matematik ödevini yapmadığını görmüştür.
Bu durumda yalnızca matematik ödevini yapan öğrenci sayısı 5 olduğuna göre her iki ödevini yapan öğrenci sayısı kaçtır?A) 11 B) 12 C) 13 D) 14 E) 15
-
A3B5 dör basamaklı sayısı 9 ile, A1B üç basamaklı sayısı 5 ile kalansız bölünebilmektedir.
Bu göre A'nın alabileceği değerler toplamı kaçtır?A) 3 B) 5 C) 8 D) 11 E) 13
-
Mehmet Bey, fiyatları eşit ve lira cinsinden tam sayı olan gömleklerin 9 tanesini 4A1 lira ödemiştir.
4A1 üç basamaklı bir doğal sayı olduğuna göre bir gömleğin fiyatı kaç liradır?A) 49 B) 48 C) 47 D) 46 E) 45
-
Doktor Mustafa 6 günde bir, hemşire Aslı 8 günde bir nöbet tutmaktadır.
İkisi birlikte Cuma günü nöbet tuttuktan sonraki 2.birlikte nöbetleri hangi gün olur?A) Salı B) Çarşamba C) Perşembe
D) Cuma E) Cumartesi -
Bilinmeyeni x olan 2x + 3(x-a) - 1 = bx + 8 denkleminin çözüm kümesi sonsuz elemanlı olduğuna göre a + b kaçtır?
A) 2 B) 3 C) 8 D) 9 E) 11
-
4(x-5) + 2(x-12) - 3(-x +3) = 1 denkleminin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir?
A) {-18} B) {-6} C) {6} D) {18} E) {-24}
-
-5x + 7 ≤ -2x -14 eşitsizliğini sağlayan x'in en küçük tam sayı değeri kaçtır?
A) 8 B) 7 C) 4 D) 3 E) 0
-
|2x - 5| - 3 < 6 eşitsizliğini sağlayan kaç tane x tam sayısı vardır?
A) 7 B) 8 C) 9 D) 10 E) 11
-
3(x-2) + x -10 = -2x - 4 denkleminin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir?
A) {2} B) {-4} C) {-6} D) R E) ∅
-
Aşağıdakileden hangisi bir irrasyonel sayıdır?
A) 0,3- B) 1,75 C) √12 D) √16 E) √25
-
olduğuna göre a + b kaçtır?
A) 10 B) 11 C) 12 D) 13 E) 14
-
||x - 4| + 2 | = 5 denkleminin çözüm kümesi aşağıdakilerden hangisisidir?
A) {-7, -1} B) {-7, 1} C) {-1, 7}
D) {1,7} E) {-1, -7} -
denklem sistemini sağlayan x değeri kaçtır?A) 16 B) 12 C) 9 D) 6 E) 4
-
işleminin sonucu kaçtır?
A) 2 B) √5 C) 3 D) 7 E) √8
Doğru cevap anahtarı C) [-2,13) olacaktır. Verilen eşitsizlik ifadesi, x'in -2 ile 13 arasında olmasını sağlar. -2 dahil olmak üzere 13 hariçtir. Bu nedenle, doğru cevap C) [-2,13) olacaktır.
Cevap Anahtarı: C) 4 1. Verilen ifadeye göre, "a3b" üç basamaklı sayısı, "3ab" üç basamaklı sayısından 90 fazla olmalıdır. 2. İki basamağı aynı olan sayıları ele alarak deneyebiliriz. Örneğin, "33" üç basamaklı sayısı, "3 x 33 = 99" üç basamaklı sayısından 90 fazladır. 3. Ancak, "a3b" üç basamaklı sayısı ve "3ab" üç basamaklı sayısı için aynı sayılar kullanılmamalıdır. Bu nedenle, "a" rakamı "3"ten farklı bir rakam olmalıdır. Yani, a = 4 olmalıdır. 4. Sonuç olarak, a = 4 olduğunda, "a3b" üç basamaklı sayısı 90 fazla olur: 433 - 343 = 90.
Doğru cevap anahtarı D) 6 olacaktır.
Doğru cevap A) -,+,- olmalıdır. İlk denklemde a^2 . b^3 > 0 olduğu belirtilmiştir. Bir sayının karesi veya küpü pozitif olduğunda, sayı kendisi pozitif veya sıfır olabilir. Bu nedenle a negatif veya sıfır olabilir, b ise pozitif veya sıfır olabilir. İkinci denklemde b^5 . c^3 < 0 olduğu belirtilmiştir. Bir sayının beşinci kuvveti veya üçüncü kuvveti negatif olduğunda, sayı kendisi negatif olmalıdır. Bu nedenle b negatif olmalıdır ve c pozitif veya sıfır olabilir. Üçüncü denklemde a - c < 0 olduğu belirtilmiştir. Bu denklem, a'nın c'den küçük olduğunu gösterir. Bu durumda a negatif ve c pozitif olmalıdır. Sonuç olarak, a negatif (-), b pozitif (+) ve c pozitif (+) olmalıdır: -,+,-.
Açıklama: a.b = 2c - 1 denkleminde sağ taraf tek sayıdır. Sol taraf ise iki tam sayının çarpımıdır. İki tam sayının çarpımı tek olabilmesi için her ikisinin de tek olması gerekir. Bu nedenle, a ve b tek sayılardır.
Doğru cevap anahtarı D) 2 olacaktır. Verilen denklem |x+2y-5| + (2x + y - 4)^2 = 0 olarak verilmiştir. Bu denklemde toplamı sıfır olan iki terim yer almaktadır. İlk olarak, mutlak değeri sıfır olan terimi inceleyelim: |x+2y-5| = 0. Bu, x + 2y - 5 ifadesinin sıfıra eşit olduğunu gösterir. İkinci terimi inceleyelim: (2x + y - 4)^2 = 0. Bu, 2x + y - 4 ifadesinin sıfıra eşit olduğunu gösterir. İki denklemi birleştirerek çözümü bulalım: a) x + 2y - 5 = 0 b) 2x + y - 4 = 0 İki denklemi çözelim: a) x = 5 - 2y b) y = 4 - 2x x ve y değerlerini birleştirerek çözümü bulalım: x = 5 - 2(4 - 2x) x = 5 - 8 + 4x -3x = -3 x = 1 y = 4 - 2(1) y = 4 - 2 y = 2 Sonuç olarak, x = 1 ve y = 2 olduğunda verilen denklemi sağlayan bir çözüm bulunur. Bu nedenle, x.y = 1 * 2 = 2, yani x.y = 2 olur.
Doğru cevap D) 2 olmalıdır. Verilen denklem |x + 2y - 5| + (2x + y - 4)^2 = 0 olarak verilmiştir. Denklemin sol tarafındaki ifade sıfır olmalıdır çünkü pozitif bir sayının mutlak değeri sıfır veya negatif olamaz. İlk terim |x + 2y - 5| ifadesi sıfır olduğunda, içindeki ifade de sıfır olmalıdır. Yani x + 2y - 5 = 0 olmalıdır. İkinci terim (2x + y - 4)^2 ifadesi sıfır olduğunda, içindeki ifade de sıfır olmalıdır. Yani 2x + y - 4 = 0 olmalıdır. Bu iki denklemi çözdüğümüzde x = 2 ve y = 1 bulunur. Sonuç olarak, x.y = 2.1 = 2 olmalıdır.
Doğru cevap anahtarı A) 0 olacaktır. Verilen denklem a.x - 3(x - 2) = 2(x + 1) + b olarak verilmiştir. Bu denklemi çözerken x'e bağlı terimleri gruplayarak çözümü bulabiliriz. Çözüm adımları: Verilen denklemi çözelim: a.x - 3x + 6 = 2x + 2 + b Benzer terimleri birleştirelim: (a - 3 - 2)x + 6 = 2x + 2 + b Katsayıları karşılaştıralım: a - 5 = 2 a = 7 a değerini denklemde yerine koyalım: 7x - 3x + 6 = 2x + 2 + b 4x + 6 = 2x + 2 + b Benzer terimleri birleştirelim: 4x - 2x = 2 + b - 6 2x = -4 + b x'e bağlı terimi çözelim: 2x = b - 4 x = (b - 4) / 2 Denklemin çözüm kümesi tüm gerçek sayılar olduğuna göre, x'in herhangi bir değer alabilmesi için (b - 4) / 2 ifadesinin herhangi bir gerçek sayıya eşit olması gerekir. Bu durumu sağlamak için b = 4 olmalıdır. Sonuç olarak, a + b = 7 + 4 = 11 olur. Bu nedenle, a + b = 11'dir.
Doğru cevap D) 1 olmalıdır. Verilen önerme p' ∧ (p' v q)' olarak verilmiştir. İç içe geçmiş parantezleri açmak ve önermeyi sadeleştirmek için öncelikle De Morgan Yasası'nı uygulayalım: (p' v q)' ifadesi p' ve q' ifadelerinin kesişimi olarak yazılabilir. p' ifadesi p'nin tersi, yani yanlış olduğunu gösterir. q' ifadesi q'nun tersi, yani yanlış olduğunu gösterir. p' ve q' ifadeleri birlikte değerlendirildiğinde, her ikisi de yanlış olduğundan, p' ∧ q' ifadesi de yanlış olacaktır. Yanlış ifadesi 0 olarak gösterildiğinden, p' ∧ q' ifadesi 0'ı temsil eder. 0' ifadesi 1'e eşittir. Sonuç olarak, en sade hali 1'dir.
Doğru cevap A) {2,{1,3},{2,3}} olmalıdır. Verilen küme A = {1,2{1,2},3,{2,3}}'dır. A kümesinin 3 elemanlı alt kümelerini kontrol edelim: {2,{1,3},{2,3}}: A kümesinin bir alt kümesidir, çünkü A kümesinin elemanlarından bazılarını içerir. {1,2,{1,2}}: A kümesinin bir alt kümesidir, çünkü A kümesinin elemanlarından bazılarını içerir. {2,3,{2,3}}: A kümesinin bir alt kümesidir, çünkü A kümesinin elemanlarından bazılarını içerir. {1,{1,2},{2,3}}: A kümesinin bir alt kümesidir, çünkü A kümesinin elemanlarından bazılarını içerir. {1,{1},{1,3}}: A kümesinin bir alt kümesidir, çünkü A kümesinin elemanlarından bazılarını içerir. Buna göre, A kümesinin 3 elemanlı alt kümelerinden biri olmayan tek seçenek {2,{1,3},{2,3}}'tür.
Toplam öğrenci sayısı 30 olduğuna göre, Türkçe ödevini yapmayan öğrenci sayısı 12 ve matematik ödevini yapmayan öğrenci sayısı 13'tür. Bu durumda, matematik ödevini yapan öğrenci sayısı 30 - 13 = 17 olacaktır. Ancak soruda belirtilen ve sadece matematik ödevini yapan öğrenci sayısı 5 olduğu için, her iki ödevini yapan öğrenci sayısı 17 - 5 = 12 olmalıdır. Bu şekilde, cevap anahtarındaki "B) 12" sonucuna ulaşılır.
Cevap anahtarı: D) 11 Verilen bilgilere göre A3B5 dör basamaklı sayısı 9 ile, A1B üç basamaklı sayısı 5 ile kalansız bölünebilmektedir. 1) A3B5 dör basamaklı sayısı 9 ile kalansız bölünebildiğine göre, sayının 9 ile tam bölünebilmesi için basamaklarının toplamının 9'a tam bölünmesi gerekmektedir. Bu durumu sağlamak için A + 3 + B + 5 toplamının 9'a tam bölünebilmesi gerekir. 2) A1B üç basamaklı sayısı 5 ile kalansız bölünebildiğine göre, sayının 5 ile tam bölünebilmesi için basamaklarının toplamının 5'e tam bölünmesi gerekmektedir. Bu durumu sağlamak için A + 1 + B toplamının 5'e tam bölünebilmesi gerekir. 3) İlk durumu göz önünde bulundurarak, A + 3 + B + 5 toplamının 9'a tam bölünebilmesi için A + B toplamının 1'e tam bölünebilmesi gerekmektedir. 4) İkinci durumu göz önünde bulundurarak, A + 1 + B toplamının 5'e tam bölünebilmesi için A + B toplamının 4'e tam bölünebilmesi gerekmektedir. 5) A + B toplamının hem 1'e hem de 4'e tam bölünebilmesi için A + B toplamının 4'ün katı olan 4, 8, 12, vb. sayılar olabileceği görülür. 6) Ancak, A ve B tam sayı olduğu için A + B toplamının 4 olması gerekmektedir. Sonuç olarak, A + B = 4 olduğu için A'nın alabileceği değerler toplamı 4 olur. Bu nedenle, A + B = 4'tür.
Cevap anahtarı: A) 49 Mehmet Bey, fiyatları eşit ve lira cinsinden tam sayı olan gömleklerin 9 tanesini 4A1 lira ödemiştir. Verilen bilgilere göre, 4A1 üç basamaklı bir doğal sayıdır. A, onlar basamağındaki rakamı temsil etmektedir. 1) 4A1 üç basamaklı bir doğal sayı olduğuna göre, A'nın alabileceği değerler 0 ile 9 arasında olabilir. 2) Ancak, fiyatlar tam sayı olduğu için A'nın alabileceği değerler yalnızca 0 ve 1 olabilir. Çünkü 4A1 ifadesi, yalnızca lira cinsinden tam sayı değerlerini temsil eder. 3) Dolayısıyla, A = 1 olmalıdır. Bu durumda bir gömleğin fiyatı 49 lira olur. Sonuç olarak, bir gömleğin fiyatı 49 liradır.
Cevap anahtarı: C) Perşembe Doktor Mustafa 6 günde bir nöbet tutuyor, hemşire Aslı ise 8 günde bir nöbet tutuyor. Cuma günü ikisi birlikte nöbet tuttuktan sonra, bir sonraki birlikte nöbetleri hangi gün olur? 1) Doktor Mustafa'nın nöbet tutma periyodu 6 gündür, yani her 6 günde bir nöbet tutar. 2) Hemşire Aslı'nın nöbet tutma periyodu 8 gündür, yani her 8 günde bir nöbet tutar. 3) İki periyodu birleştirdiğimizde, en küçük ortak katlarını bulmamız gerekmektedir. Ortak katlarını bulmak için iki periyodun çarpımını alabiliriz. 6 x 8 = 48 4) Sonuç olarak, ikisi birlikte nöbet tuttuktan sonra bir sonraki birlikte nöbetleri 48 gün sonra tekrar aynı güne denk gelecektir. 5) Cuma günü ikisi birlikte nöbet tuttuktan sonra, 48 gün sonrasında hangi gün olduğunu bulmak için Cuma gününe 48 gün ekleyebiliriz. Cuma + 48 gün = Perşembe Sonuç olarak, ikisi birlikte nöbet tuttuktan sonra 2. birlikte nöbetleri Perşembe günü olacaktır.
Cevap anahtarı: A) 2 Verilen denklem 2x + 3(x-a) - 1 = bx + 8 şeklindedir. 1) Denklemin çözüm kümesinin sonsuz elemanlı olduğu belirtilmiştir. Bu durum, denklemin her x değeri için geçerli olduğunu gösterir. 2) Denklemi çözmek için, terimleri toplamamız ve benzer terimleri bir araya getirmemiz gerekmektedir. 2x + 3x - 3a - 1 = bx + 8 5x - 3a - 1 = bx + 8 3) Denklemin çözüm kümesinin sonsuz elemanlı olması, x'in her değeri için geçerli olması anlamına gelir. Bu durumu sağlamak için, her iki tarafın da aynı katsayıya sahip olması gerekmektedir. 5 = b 4) Ayrıca, a + b = -3a - 1 = 8 olmalıdır. -3a - 1 + a = 8 -2a - 1 = 8 -2a = 9 a = -9/2 5) Sonuç olarak, a + b = -9/2 + 5 = 1/2 a + b = 2/2 Sonuç olarak, a + b = 1 veya 2 olur.
Sorunun cevap anahtarı "C) {6}" olarak belirlenmiştir. Çözüm açıklaması şu şekildedir: Verilen denklemi çözmek için öncelikle parantezleri açarız. Bu işlem sonucunda elde edilen ifade: 4x - 20 + 2x - 24 + 3x - 9 = 1 şeklinde olur. Benzer terimleri topladığımızda ise: 9x - 53 = 1 elde ederiz. Denklemi çözmek için iki tarafı da 53'e ekleriz: 9x = 54. İki tarafı da 9'a bölersek, x = 6 elde ederiz. Bu durumda, gerçek sayılardaki çözüm kümesi sadece {6}'dır.
Verilen eşitsizliği çözmek için öncelikle benzer terimleri bir araya getiririz. Bu durumda, -5x + 7 ≤ -2x - 14 eşitsizliğini elde ederiz. Ardından, -2x terimini diğer tarafa geçirmek için her iki tarafı da -2x ile çıkarırız. Bu işlem sonucunda -5x + 2x + 7 ≤ -14 elde ederiz. Benzer terimleri topladığımızda ise -3x + 7 ≤ -14 şeklinde bir ifadeye ulaşırız. Daha sonra, 7 terimini diğer tarafa geçirmek için her iki tarafı da -7 ile azaltırız. Bu işlem sonucunda -3x ≤ -21 elde ederiz. Son olarak, denklemdeki x'in katsayısı olan -3'ü her iki tarafa da böleriz. Bu durumda, x ≥ 7 şeklinde bir eşitsizlik elde ederiz. En küçük tam sayı değerini bulmak için x'in en küçük olabileceği durumu göz önünde bulundururuz. Bu durumda, x = 7 olmalıdır. Bu şekilde, cevap anahtarındaki "B) 7" sonucuna ulaşılır.
Sorunun doğru cevap anahtarı "B) 8" olacaktır. Çözüm açıklaması şu şekildedir: Verilen eşitsizliği çözmek için mutlak değeri içeren ifadeyi açmamız gerekmektedir. Bu durumda, |2x - 5| - 3 < 6 eşitsizliğini elde ederiz. Mutlak değeri açmak için iki durumu ele alırız: Durum: 2x - 5 ≥ 0 (mutlak değer ifadesi pozitif veya 0 olabilir) Bu durumda, mutlak değeri açmak için |2x - 5| ifadesi 2x - 5 olarak yazılır. Eşitsizlik şu şekilde oluşur: 2x - 5 - 3 < 6. İfadeyi çözmek için benzer terimleri toplarız ve x'i buluruz: 2x - 8 < 6, 2x < 14, x < 7. Bu durumda, x'in değeri 7'den küçük olmalıdır. Durum: 2x - 5 < 0 (mutlak değer ifadesi negatif olabilir) Bu durumda, mutlak değeri açmak için |2x - 5| ifadesi -(2x - 5) olarak yazılır. Eşitsizlik şu şekilde oluşur: -(2x - 5) - 3 < 6. İfadeyi çözmek için benzer terimleri toplarız ve x'i buluruz: -2x + 5 - 3 < 6, -2x + 2 < 6, -2x < 4, x > -2. Bu durumda, x'in değeri -2'den büyük olmalıdır.
Cevap anahtarı: A) {2} Verilen denklem 3(x-2) + x - 10 = -2x - 4 şeklindedir. 1) Denklemi çözmek için, terimleri toplamamız ve benzer terimleri bir araya getirmemiz gerekmektedir. 3x - 6 + x - 10 = -2x - 4 4x - 16 = -2x - 4 2) Denklemi çözmek için, x'in katsayıları bir tarafa, sayı terimlerini diğer tarafa taşıyarak devam edelim. 4x + 2x = 16 - 4 6x = 12 x = 2 3) Sonuç olarak, denklemin çözüm kümesi x = 2'den oluşur.
Sorunun doğru cevap anahtarı "A) 0,3^-" olacaktır. Çözüm açıklaması şu şekildedir: İrrasyonel sayılar, kesirli bir şekilde ifade edilemeyen ve sonsuz ondalık kesir olarak ifade edilemeyen sayılardır. Verilen seçenekler arasında sadece 0,3^- irrasyonel bir sayıdır. Çünkü 0,3^- sayısı tam olarak kesirli bir ifadeyle ifade edilemez ve ondalık kesir olarak sonsuz bir desimal kesire dönüşür. Diğer seçenekler (B) 1,75, (C) √12, (D) √16 ve (E) √25, hepsi rasyonel sayılardır, yani kesirli bir şekilde ifade edilebilirler.
Cevap anahtarı: A) 10
Sorunun doğru cevap anahtarı "C) {-1, 7}" olacaktır. Çözüm açıklaması şu şekildedir: Verilen denklemi çözmek için mutlak değer ifadesini açmamız gerekmektedir. Bu durumda, ||x - 4| + 2 | = 5 denklemini elde ederiz. İlk olarak, içteki mutlak değeri açarız: |x - 4| + 2 = 5. Ardından, dıştaki mutlak değeri açarız: x - 4 + 2 = 5 veya -(x - 4) + 2 = 5. İlk durumda, x - 4 + 2 = 5 eşitliğini çözeriz: x - 2 = 5, x = 7. Bu durumda, x'in değeri 7'dir. İkinci durumda, -(x - 4) + 2 = 5 eşitliğini çözeriz: -x + 4 + 2 = 5, -x + 6 = 5, -x = -1, x = 1. Bu durumda, x'in değeri 1'dir.
Sorunun cevap anahtarı "D) 6" olarak belirlenmiştir. Çözüm açıklaması şu şekildedir: Verilen denklem sistemi iki denklem içerir. İlk denklem: 3x - 2y = 10, ikinci denklem ise: 4x + y = 16. Bu denklem sisteminde, x ve y değerlerini bulmak için denklemleri çözebiliriz. İlk adımda, ikinci denklemi çözmek için y'yi elde ederiz: y = 16 - 4x. Daha sonra, y'nin değerini birinci denkleme yerleştiririz: 3x - 2(16 - 4x) = 10. Bu denklemi çözmek için terimleri toplarız: 3x - 32 + 8x = 10. Benzer terimleri bir araya getiririz ve x'i buluruz: 11x - 32 = 10, 11x = 42, x = 6. Son olarak, x'in değerini ikinci denklemde yerine koyarız: y = 16 - 4(6), y = 16 - 24, y = -8. Bu şekilde, verilen denklem sistemini sağlayan x değeri 6'dır.
Cevap anahtarı: C) 3
Yorum Bırak
Evet ne yapam
2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test Detayları
2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test 25 kere indirildi. Bu sınav Zor derecede zorluktadır. Sınav zorluk derecesi sınavı oluşturan soruların istatistikleri alınarak oluşturulmuştur. Toplamda 24 sorudan oluşmaktadır. Sınav soruları aşağıda verilen kazanımları ölçecek şekilde hazırlanmıştır. 15 Aralık 2022 tarihinde eklenmiştir. Bu sınavı şimdiye kadar 1 kullanıcı beğenmiş. Bu sınavı çözerek başarınızı artırmak için 2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test Testini Çöz tıklayın. 2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test yazılı sınavına henüz hiç yorum yapılmamış. İlk yorum yapan siz olun.2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test sınavında hangi soru türleri kullanılmıştır?
Bu sınavda verilen soru türleri kullanılmıştır.- Test
2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test Hangi Kazanımları Kapsıyor?
Bu sınav ve tema ve kazanımlarını kapsamaktadır.- DENKLEM VE EŞİTSİZLİKLER
- Birinci Dereceden Denklem ve Eşitsizlikler
- Denklem ve Eşitsizliklerle ilgili Uygulamalar
- Üslü ifadeler ve Denklemler
Ayrıca 2022-2023 9.sınıf matematik dersi 1.dönem 2.yazılı soruları; tamamı test ve cevap anahtarlı olarak yeni müfredat uygun hazırlanmıştır
Eşitsizliklerin çözüm kümesini anlamak ve bu kümenin nasıl temsil edildiğini tanımak.
Matematiksel ifadeleri anlama ve denklemleri çözme becerisi.
Çözüm açıklaması: Verilen denklem 2a + 3b = 27 şeklinde ifade edilmiştir. a ve b pozitif tam sayılar olduğu belirtilmiştir. Eşitliği sağlayan (a, b) ikililerini bulmak için uygun değerleri deneyebiliriz. Denklemin çözüm kümesi için uygun olan pozitif tam sayı çiftleri: (6, 5) --> 26 + 35 = 12 + 15 = 27 (9, 3) --> 29 + 33 = 18 + 9 = 27 (12, 1) --> 212 + 31 = 24 + 3 = 27 (15, -1) --> 215 + 3(-1) = 30 - 3 = 27 (18, -3) --> 218 + 3(-3) = 36 - 9 = 27 (21, -5) --> 221 + 3(-5) = 42 - 15 = 27 Verilen eşitliği sağlayan ikililer (6, 5), (9, 3), (12, 1), (15, -1), (18, -3) ve (21, -5) olduğu görülür. Bu nedenle, toplamda 6 farklı (a, b) ikilisi bulunur.
İki veya daha fazla denklemi birleştirerek denklem sistemlerini çözebilme becerisi ve reel sayıların işaretlerini belirleme yeteneği.
Denklemleri analiz ederek, sayıların çift veya tek olma durumlarını belirleme becerisi.
Denklemi sağlayan değerleri bulma ve bu değerleri kullanarak ifadeyi hesaplama.
Denklemleri analiz ederek, bilinmeyenlerin değerlerini bulma becerisi ve matematiksel ifadeleri çözme yeteneği.
Denklemdeki bilinmeyenleri çözme, terimleri gruplama ve denklemin çözüm kümesini bulma.
Mantıksal ifadeleri sadeleştirme ve önerme mantığına ilişkin kavramları anlama.
Küme teorisi ve alt küme kavramını anlama.
matematik ve Türkçe ödevlerini doğru şekilde anlama ve sayma becerisidir.
Sayıların bölünebilme özelliklerini kullanma, basamaklarının toplamlarını hesaplama ve tam bölünebilme koşullarını değerlendirme.
Basamak değerlerini anlama, fiyatların tam sayı olduğunu dikkate alma ve doğru sonuca ulaşma.
İki farklı periyodu birleştirme, en küçük ortak katı bulma ve doğru günü hesaplama.
Denklemi çözme, terimleri bir araya getirme, katsayıları karşılaştırma ve doğru sonuca ulaşma.
Denklemleri çözme ve denklemde verilen ifadeleri matematiksel işlemlerle dönüştürme becerisidir.
Eşitsizlikleri çözme ve matematiksel ifadeleri doğru bir şekilde dönüştürme becerisidir.
Sonuç olarak, x'in 7'den küçük olması ve -2'den büyük olması gerekmektedir.
Denklemi çözme, terimleri bir araya getirme, doğru sonuca ulaşma.
İrrasyonel sayıları tanıma ve rasyonel-irrasyonel sayılar arasındaki farkı anlama becerisidir.
Denklemi çözme, faktörleri analiz etme, doğru sonuca ulaşma.
Mutlak değerli denklemleri çözme becerisidir.
Denklem sistemlerini çözme ve denklemlerdeki bilinmeyenleri bulma becerisidir.
Köklü ifadeleri basitleştirme, doğru sonuca ulaşma.
etiketlerini kapsamaktadır.Hangi kategoriye ait?
2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test sınavı 9.Sınıf kategorisinin Matematik alt kategorisinin, 1 dönemine ait.2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test Testi İstatistikleri
Bu sınav 62 kere çözüldü. Sınava kayıtlı tüm sorulara toplamda 145 kere doğru, 423 kere yanlış cevap verilmiş.2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test Sınavını hangi formatta indirebilirim?
2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test sınavını .pdf veya .docx olarak ücretsiz indirebilirsiniz. Bunun yanında sistem üzerinden doğrudan yazdırabilirsiniz. Veya öğretmen olarak giriş yaptıysanız 2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test sınavını sayfanıza kaydedebilirsiniz.2022-2023 9.Sınıf Matematik 1.Dönem 2.Yazılı - Test sınav sorularının cevap anahtarlarını nasıl görebilirim?
Sınavın cevap anahtarını görebilmek için yukarıda verilen linke tıklamanız yeterli. Her sorunun cevabı sorunun altında gösterilecektir. Veya Sınavı .docx olarak indirdiğinizde office word programıyla açtığınızda en son sayfada soruların cevap anahtarına ulaşabilirsiniz.Kendi Sınavını Oluştur
Değerli öğretmenlerimiz, isterseniz sistemimizde kayıtlı binlerce sorudan 9.Sınıf Matematik dersi için sınav-yazılı hazırlama robotu ile ücretsiz olarak beş dakika içerisinde istediğiniz soru sayısında, soru tipinde ve zorluk derecesinde sınav oluşturabilirsiniz. Yazılı robotu için Sınav Robotu tıklayın.
Sınav hakkında telif veya dönüt vermek için lütfen bizimle iletişime geçin.